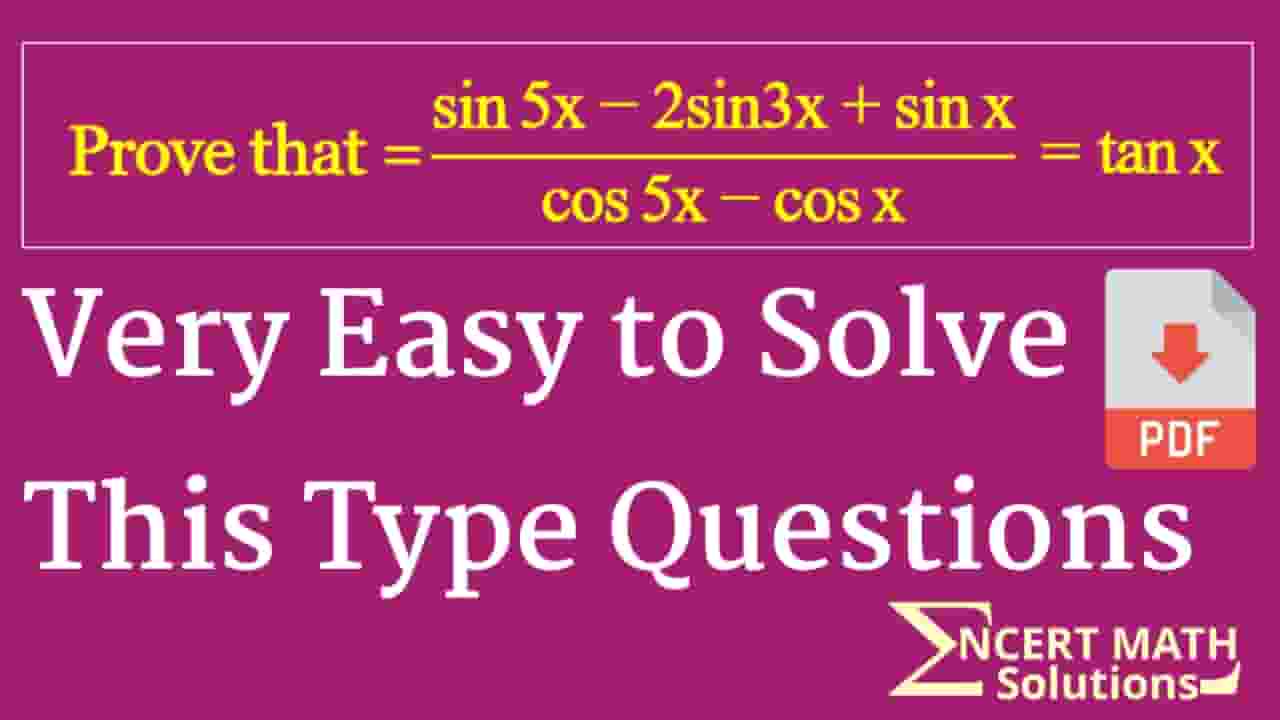Dear students, if you want the NCERT Math solutions of Prove That sin5x 2sin3x sinx cos5x cosx tanx, then read this article completely because today I am going to solve it in a better way.
If you people read this completely, then I can say with the full claim that you will not have any doubt in your mind because I will tell you the best way to solve it.
Dear students, what I am going to explain to you today is the example of chapter number 3 of NCERT Math Solutions Class 11. You guys get to see this question in Example 17 of Trigonometry Functions in Class 11.
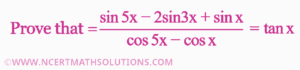
Apart from this, keep one more thing in mind many questions are asked from examples in the board exam, so practice this question well so that you do not miss this question. In the previous article, I explained an important question Prove That Root 3 is an Irrational Number to you very easily, in the same way, we will understand today’s question as well.
Let us know the correct solution of Prove That sin5x 2sin3x sinx cos5x cosx tanx and we will also know how to solve this type of question so that you can solve this type of question very easily.
Prove That sin5x 2sin3x sinx cos5x cosx tanx or (sin5x-2sin3x+sinx)/(cos5x-cosx)=tanx
Dear students, we have to prove tanx, for this, we will use some formulas and you are very well familiar with these formulas. I will write this formula while doing Prove That (sin5x-2sin3x+sinx)/(cos5x-cosx)=tanx on the same page so that you guys can understand every little thing very well.
Let us now solve this question and that too in a step-by-step manner so that we can understand each and every concept very well. This question comes in 5 marks in board exams sometimes so this question is very important.

Solutions: Prove That (sin5x-2sin3x+sinx)/(cos5x-cosx)=tanx we will first write the left-hand side then use the formula of sinC + sinD in sin5x+sinx and cosC-cosD in cos5x-cosx.
L.H.S = (sin5x-2sin3x+sinx)/(cos5x-cosx)
L.H.S = (sin5x+sinx−2sin3x)/(cos5x-cosx)
Because, sinC + sinD = {2sin(C+D)\2}×{cos(C−D)\2} And cosC−cosD = {−2sin(C+D)\2}×{sin(C−D)\2}, Therefore we apply this formula in LHS then,
L.H.S = [{2sin(5x+x)\2}×{cos(5x−x)\2}−2sin3x]÷{−2sin(5x+x)\2}×{sin(5x−x)\2}
= [{2sin(6x)\2}×{cos(4x)\2}−2sin(3x)]÷{−2sin(6x)\2}×{sin(4x)\2}
= [{2sin(3x)}×{cos(2x)}−2sin(3x)]÷{−2sin(3x)}×{sin(2x)}
Taken common 2sin(3x) then,
= 2sin(3x){cos(2x)−1}÷{−2sin(3x)}×{sin(2x)}
numerator and denominator have 2sin(3x) so they will cancel each other out, then
= {cos(2x)−1}÷{−{sin(2x)}
= {cos(2x)−1}÷{−{sin(2x)}
Taken common (−) then,
= −{1−cos(2x)}÷{−{sin(2x)}
We already know that 1−cos(2x) = 2sin²x and sin(2x) = 2sinx.cosx, So
= −{2sin²x}÷{−2sinx.cosx}
Now, −2sinx from the numerator and the denominator will cancel each other out, then
= {sinx}÷{cosx}
= sinx/cosx
= tanx
= R.H.S
Hence Proved That (sin5x-2sin3x+sinx)/(cos5x-cosx)=tanx
So dear students, here we have learned how to solve Prove That sin5x 2sin3x sinx cos5x cosx tanx. I have proved this question very easily above and I hope that now there will be no doubt in your mind.
To prove that (sin5x+sinx-2sin3x)/(cos5x-cosx) = tanx, we can use several trigonometric identities, including:
- sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
- cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
- sin(2a) = 2sin(a)cos(a)
- sinC + sinD = {2sin(C+D)\2}×{cos(C−D)\2}
- cosC−cosD = {−2sin(C+D)\2}×{sin(C−D)\2}
- 1−cos(2x) = 2sin²x
- sin(2x) = 2sinx.cosx
All the above formulas are very important, out of which the following four formulas have been used to prove your today’s question, rest of the formulas will also help you to solve the next question.
Students, this article is very useful for you, share it with all your friends also because they may also need it. You will find the solution to many such maths questions on this blog, you people can come and check this blog.
I hope that you will have no difficulty in proving that (sin5x-2sin3x+sinx)/(cos5x-cosx)=tanx. I will soon provide you with solutions to more important questions so that you can prepare better for your upcoming exams.
What is the first step in proving the identity (sin5x-2sin3x+sinx)/(cos5x-cosx)=tanx?
The first step is to simplify the left-hand side of the equation using trigonometric identities.
Which identities are useful for simplifying the left-hand side of the equation?
The following identities are useful for simplifying the left-hand side of the equation:
sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
sin(a-b)=sin(a)cos(b)-cos(a)sin(b)
cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
cos(a-b)=cos(a)cos(b)+sin(a)sin(b)
How do you apply these identities to simplify the left-hand side of the equation?
To simplify the left-hand side of the equation, you can use the sin(a+b) and sin(a-b) identities to expand sin5x and sin3x, and the cos(a+b) and cos(a-b) identities to expand cos5x and cosx.
What is the next step after simplifying the left-hand side of the equation?
The next step is to divide both sides of the equation by cosx, since the right-hand side is equal to tanx.
What should be done if there is a factor of (cos5x-cosx) in the denominator of the left-hand side of the equation?
If there is a factor of (cos5x-cosx) in the denominator of the left-hand side of the equation, you can use the identity cos(a)-cos(b)=-2sin[(a+b)/2]sin[(a-b)/2] to factor it.
How do you check if the identity (sin5x-2sin3x+sinx)/(cos5x-cosx)=tanx is true?
To check if the identity is true, you can substitute different values of x into both sides of the equation and verify that they are equal. Alternatively, you can manipulate the left-hand side of the equation until it is equivalent to the right-hand side using trigonometric identities.