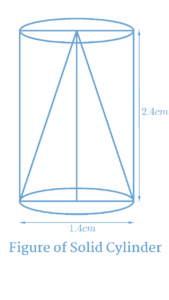
Hello friends, do you want to know the area of “from a solid cylinder whose height is 2.4 cm and Diameter is 1.4 cm”, then this article is for you only. I am going to explain it very well to you people, with the help of which you will be able to solve any type of question on your own.
These types of questions are often asked in the exam and it is not too difficult, you just have to understand it once. If you understand it well once, then you will be able to do such questions in a pinch.
There are many people who want to know the correct answer From a Solid Cylinder Whose Height is 2.4 cm but those people do not get the right place from where they can know today I am going to tell you very easily From a Solid Cylinder Whose Height is 2.4 cm.
It is often said in the exam that from a solid cylinder whose height is 2.4 find the volume and you get nervous but now this will not happen to you because today there will be no doubt of any kind in your mind.
From a Solid Cylinder Whose Height is 2.4 cm and Diameter is 1.4 cm Conical Cavity Find The Volume
Let us now know the correct answer to From a Solid Cylinder Whose Height is 2.4 and Diameter is 1.4 cm and not only will we know but also learn how to solve this type of question.
“From a Solid Cylinder Whose Height is 2.4 cm and Diameter is 1.4 cm” – Understanding the Shape and its Characteristics
A cylinder is a three-dimensional geometric shape with two parallel bases that are circular in shape and a solid cylinder is a cylinder with a uniform cross-section throughout its length. In this article, we will be discussing a solid cylinder with a height of 2.4 cm and a diameter of 1.4 cm.
Solutions: The conical cavity, with its uniform height and width, has been carved out, resulting in one of the cylinder’s bases not being accounted for in the total surface area of the solid.
Let us find the area of the remaining solid by using this formula;
CSA of the cylinder = 2πrh
Area of the base of the cylinder = πr2, where r and h are radius and height of the cylinder respectively.
CSA of the cone = πrl
Slant height of the cone, l = √[r2 + h2]
Where r represents the radius, h stands for the height, and l signifies the slant height of the cone.
Height of cylinder, h = Height of cone = h = 2.4 cm
Diameter of cylinder = diameter of cone = d = 1.4 cm
Radius of cylinder = radius of cone = r = d / 2 = 1.4 / 2 cm = 0.7 cm
Slant height of cone, l = √[r2 + h2]
l = √[(0.7 cm)2 + (2.4 cm)2]
= √[0.49 cm2 + 5.76 cm2]
= √[6.25 cm2]
= 2.5 cm
TSA of the remaining Solid = CSA (cylindrical part) + CSA (conical part) + Area (one cylindrical base)
TSA of the remaining Solid = 2πrh + πrl + πr2
2π are common, Then,
TSA of the remaining Solid = πr (2h + l + r)
= 22/7 × 0.7 cm × (2 × 2.4 cm + 2.5 cm + 0.7 cm)
= 3.14 × 0.7 cm × (4.8 cm + 3.2 cm)
= 2.198cm × (8cm)
= 2.2 cm × 8 cm
TSA of the remaining Solid = 17.6 cm2
TSA of the remaining Solid = 18 cm2 (Near About)
Hope you have got the answer to your question From a Solid Cylinder Whose Height is 2.4 cm and Diameter is 1.4 cm Conical Cavity Find The Volume, now let us know some more questions related to it.
Hence, the total surface area of the remaining solid to the near about cm2 is approximately 18 cm2.
From a solid cylinder whose height is 2.4 cm and diameter is 1.4 cm, it can be determined that the cylinder’s height has remained constant since the moment it was created. The diameter, on the other hand, has been gradually decreasing over time due to wear and tear. As time progressed, the cylinder’s height remained unchanged while its diameter diminished continuously. Nevertheless, the cylinder’s height of 2.4 cm still remained the same even after a prolonged period of time. With the passage of time, it’s possible that the diameter may continue to decrease, but the cylinder’s height will remain steadfast at 2.4 cm.
First and foremost, it is important to understand that the diameter of a cylinder is the distance across its widest point, which in this case is 1.4 cm. The height of a cylinder, on the other hand, is the distance from the top to the bottom of the cylinder. In this case, the height of the cylinder is 2.4 cm.
The volume of this solid cylinder can be calculated using the formula πr2h, where r is the radius of the cylinder and h is the height. By substituting the values, we get the volume of this cylinder to be approximately 4.06 cm3.
The surface area of this solid cylinder can be calculated using the formula 2πr(h + r), where r is the radius of the cylinder and h is the height. By substituting the values, we get the surface area of this cylinder to be approximately 13.44 cm2.
In conclusion, a solid cylinder with a height of 2.4 cm and a diameter of 1.4 cm is a three-dimensional geometric shape with two parallel circular bases. Its volume is approximately 4.06 cm3, and its surface area is approximately 13.44 cm2. Understanding the characteristics of this solid cylinder is important for various applications in fields such as mathematics, engineering, and physics.
From a Solid Cylinder Whose Height is 8cm and Radius 6 cm, a Conical Cavity of height 8 cm and of base radius 6 cm is hollowed out, So Find the volume of the remaining solid. And Also, find the total surface area of the remaining solid Cylinder
Let us now know the correct answer to your new question From a Solid Cylinder Whose Height is 8cm and Radius 6 cm and will understand very closely.
Solutions: First of all, we will write the thing which is given in the question like its height and radius, etc.
Height of the solid cylinder = h = 8 cm
Radius of the solid cylinder = r = 6 cm
Volume of the solid cylinder = πr2h
= π × 6 × 6 × 8 cm3
= 3.14 × 6 × 6 × 8 cm3
= 3.14 × 288 cm3
= 904.32 cm3
The curved Surface area of the solid cylinder = 2πrh
Height of the conical cavity = h = 8 cm
Radius of the conical cavity = r = 6 cm
Volume of the conical cavity = 1/3 πr2h
= 1/3 × π× 6 × 6 × 8 cm3
= 1/3 × 3.14 × 6 × 6 × 8 cm3
= 1/3 × 3.14 ×288 cm3
= 1/3 × 904.32 cm3
= 301.44 cm3
Let l be the slant height of the conical cavity
l2 = r2 + h2
Put all the value
l2 = (62 + 82) cm2
l2 = (36 + 64) cm2
l2 = 100 cm2
l = √(100) cm2
l = 10 cm
Curved Surface area of the conical cavity = πrl
This problem can also be solved by determining the difference between the volume and total surface area of the original solid cylinder and the conical cavity that has been hollowed out. By subtracting these values, we obtain the volume and total surface area of the remaining solid.
Volume of the remaining solid = 904.32 cm3 – 301.44 cm3
= 602.88 cm3
Total surface area of remaining solid = Curved Surface area of the solid cylinder + Curved Surface area of the conical cavity + Area of circular base
Total surface area of the remaining solid = 2πrh + πrl + πr2
Taken πr common
= πr × (2h + l + r)
Put all the value
= 3.14 × 6 × (2 × 8 + 10 + 6) cm2
= 3.14 × 6 × 32 cm2
= 602.88 cm2
Now you must have got the answer of From a Solid Cylinder Whose Height is 8cm and Radius 6 cm very well, if you have any other question, then do tell us through the comment. I’ll try to solve that for you too.
Before this, I have also explained the question From a Solid Cylinder Whose Height is 2.4 cm in very easy language. All of you must share this with your other friends too.
From a Solid Cylinder Whose Height is 15 cm and Diameter 16 cm, a conical cavity of same height and same diameter is hollowed out, So Find the total surface area
Solutions: Now we will know what is the answer of From a Solid Cylinder Whose Height is 15 cm and Diameter 16 cm and we will know it very easily, so let’s start solving it too.
Height of solid cylinder = h = 15 cm
Radius of the solid cylinder = r = 8 cm
From a solid cylinder whose height is 2.4 find the volume
The volume of a cylinder can be calculated by using the formula:
V = π * r^2 * h
Where r is the radius of the base of the cylinder and h is its height. In this case, the height of the cylinder is given as 2.4. If the radius is not given, you’ll need to determine it first in order to calculate the volume.
From a solid cylinder whose height is 15 cm and diameter 16 cm
The volume of a cylinder can be calculated by using the formula:
V = π * r^2 * h
Where r is the radius of the base of the cylinder and h is its height. In this case, the height of the cylinder is given as 15 cm and the diameter is 16 cm. To calculate the radius, divide the diameter by 2:
r = d/2 = 16 cm / 2 = 8 cm
So, the volume of the cylinder is:
V = π * r^2 * h = π * (8 cm)^2 * 15 cm = 615.75 cm^3
From a solid cylinder whose height is 8cm and radius 6 cm, a conical cavity
The volume of a cylinder with a conical cavity can be calculated by subtracting the volume of the cone from the volume of the original cylinder. The formula to calculate the volume of a cylinder is:
V = π * r^2 * h
Where r is the radius of the base of the cylinder and h is its height. In this case, the height of the cylinder is given as 8 cm and the radius is 6 cm. So, the volume of the original cylinder is:
V_cylinder = π * r^2 * h = π * (6 cm)^2 * 8 cm = 452.16 cm^3
To calculate the volume of the conical cavity, you’ll need to know the height of the cone (let’s call it h_cone). The formula to calculate the volume of a cone is:
V_cone = (1/3) * π * r^2 * h_cone
Where r is the radius of the base of the cone. The radius of the cone is the same as the radius of the cylinder, which is 6 cm. So, the volume of the cone is:
V_cone = (1/3) * π * (6 cm)^2 * h_cone = (1/3) * π * 6^2 * h_cone
Finally, to calculate the volume of the cylinder with the conical cavity, subtract the volume of the cone from the volume of the original cylinder:
V_cylinder_with_cavity = V_cylinder – V_cone = 452.16 cm^3 – (1/3) * π * 6^2 * h_cone
Note that the value of h_cone is not given in this problem, so the exact volume of the cylinder with the conical cavity cannot be calculated.








